论文背景
键值存储被广泛应用于各个领域,目前大多数的键值存储系统(如RocksDB、LevelDB等)采用LSM-Tree作为底层存储结构。关于LSM-Tree的总体设计思想这里就不再多做赘述。这里主要探讨LSM-Tree的数据合并(通常也被称作Merge或Compaction)策略。Merge过程是目前LSM-Tree的一大性能瓶颈,其能在很大程度上影响LSM-Tree的读写性能。在当今所有LSM-Tree架构的设计中,Compaction主要有分为两种策略:Tiering和Leveling。下面将简要描述一下两种策略的设计和它们之间的优劣。
Tiering vs. Leveling
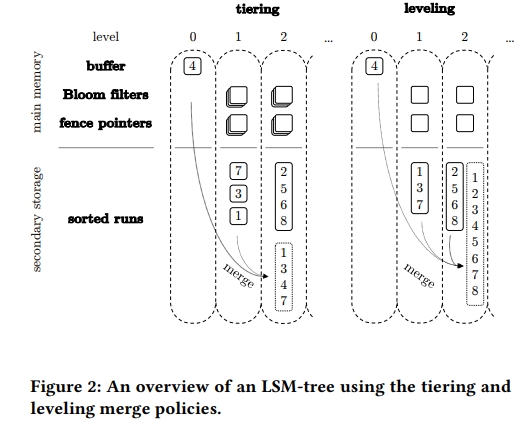
1. Tiering-Compaction
Tiering-Compaction(典型代表Cassandra)将会在某层的数据量达到阈值时合并该层的SortedRun(即一个排序单元,一个SortedRun的数据不存在重叠且有序排列)。在Tiering-Compaction的策略下,一层可能会存在多个SortedRun,即同层的数据之间可能存在重叠,因此Tiering同时还会带来读放大的问题。
2. Leveling-Compaction
与Tiering不同,Leveling-Compaction(典型代表RocksDB、LevelDB)可能会合并两层的SortedRun,该策略确保每层只有一个SortedRun,因此相比Tiering,Leveling的读放大问题相对比较小,但是同时也因为要确保每层的数据不存在重叠,Leveling会更加频繁地进行数据合并,所以Leveling会带来更加严重的写放大问题。
总结
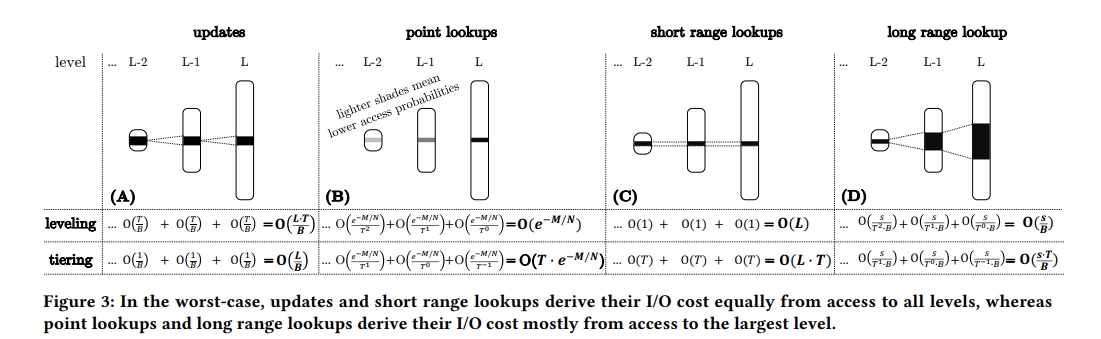
总结以上两种Compaction策略,Tiering在更新密集型工作负载下有着更大的优势(写放大小),但是在点查、长短范围查询的负载下Leveling表现更佳优异(读放大更小),同时Tiering相比Leveling空间放大的问题更加严重。
层数设定
关于LSM-Tree的层数的设定,文章中给出了下面的公式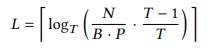
其中N表示总键值对的数量,B表示数据块(block)中所能包含的最大键值对数,P表示缓冲区中block的个数,T表示层之间的容量放大倍数,L表示根据计算得到LSM-Tree的合理层数。文中对于上面公式的解释是,Level0的容量大小表示为B*P,从而可以推出Leveli的容量大小为B*P*T^i个键值对,LSM-Tree的总数据量为N,那么最大层中大约将包含N*(T-1)/T个键值对,那么可以得出B*P*T^L = N*(T-1)/T,从而可以推导出上面的公式。并且还能推算出放大倍数T的范围为[2, N/(B*P)]。
通常来说,当Leveling(Tiering)的T增加时,其查询的性能以及空间放大问题就会降低(增加),而更新操作的开销则会增加(降低)。
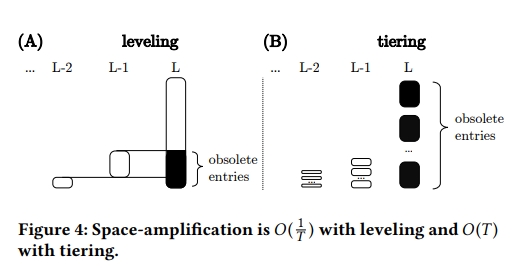
上图是作者对Tiering和Leveling空间放大率的分析。这里定义键值存储系统的空间放大率是存储的总键值对个数除以unique键值对(即不重叠数据的大小)再减去1。对于Leveling来说,最坏情况每次更新一个键值对时从第1层到第L层都存有一个key值与更新数据相同的数据,以此类推到第L层,就可能有1/T个垃圾数据对,因此总空间放大就是O(1/T);对于Tiering来说,最坏情况就是第1层到第L-1层的数据都与最后一层(第L层)存在重叠,换而言之就是最后一层中包含了系统整体key值范围的数据(不过都是垃圾数据),因此总空间放大最后一层数据量与就是O(T)。
Lazy Leveling Compaction
综上所述,Tiering和Leveling都有各自的优劣,分别适用于不同的工作负载。为了结合两种策略的优势,让系统能够适应各种工作负载,作者提出了一种Lazy Leveling的数据合并策略,该策略可以看作是Tiering和Leveling的结合体。Lazy Leveling的具体做法是在最大层采用Leveling策略合并数据(确保最大层只有一个SortedRun),而其他层使用Tiering。另外,为了加速点查,作者为不同层的布隆过滤器(Bloom Filter)分别使用了不同的内存分配(布隆过滤器的假阳率主要跟其位数组大小、哈希函数有关,通过提升位数组的大小能够有效降低假阳率)。
各负载复杂度对比
下图为Tiering、Leveling和Lazy Leveling在各负载下在最坏情况下的复杂度对比
可以看到Lazy Leveling在达到了与Leveling相同的空间放大、点查、长范围查找复杂度的同时降低系统更新的开销、以及稍逊色于Leveling的短范围查询性能。
Fluid LSM-Tree
Fluid LSM-tree是LSM-Tree的泛化,通过分别控制最大级别和所有其他级别的合并频率,允许在设计空间中流动。相对于Lazy Leveling,Fluid LSM-tree可以通过减少最大级别的合并来优化更新,或者通过在所有其他级别进行更多合并来优化短范围查找。
Fluid LSM-Tree提供了两个参数K和Z,Z表示最大层SortedRun个数,K则为其余层的最大SortedRun个数:
- K = 1, Z = 1时则为Leveling
- K = T - 1, Z = T - 1时则为Tiering
- K = T - 1, Z = 1时则为Lazy Leveling。
通过动态地调整Z和K,Fluid LSM-Tree可以在Lazy Leveling, Tiering和Leveling之间转换:增加Z可以降低最大层数据合并的频率,从而降低更新的开销;降低K可以增加其余层的合并频率,从而提升点查、短范围查询的性能。
