前缀树（Trie，又称字典树）是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。与二叉树不同，键并不是直接保存在节点中，而是由节点在树中的位置决定。

主要应用场景：自动补完、拼写检查

来源：LeetCode剑指offer II 062.实现前缀树

相关题目：LeetCode--472.连接词

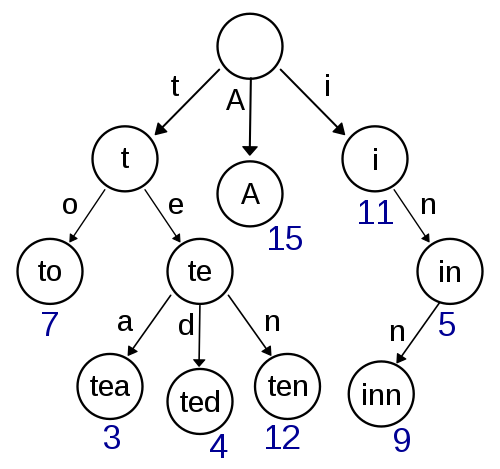
主要操作

前缀树类提供一下方法：

• Trim()：初始化前缀树
• insert(word String)：向前缀树插入字符串word
• search(word String) bool：如果字符串word在前缀树中，返回true；否则返回false
• startsWith(prefix String) bool：如果之前已经插入的字符串word的前缀之一为prefix，返回true，否则返回false

插入操作

从树的根开始插入字符串，对于当前子节点有两种情况：

• 子节点存在：沿着指针移动到子节点处，继续处理下个字符
• 子节点不存在：创建一个新的子节点，记录在children数组的对应位置上，然后沿着指针移动到子节点，继续搜索下一个字符。

重复以上步骤直到处理到字符串的最后一个字符，然后将当前节点标记为字符串的结尾。

查找前缀

从树的根开始，查找前缀。对于当前字符对应的节点，存在两种情况：

• 子节点存在：沿着指针移动到子节点，继续搜索下一个字符。
• 子节点不存在：说明树中不包含该前缀，返回一个空指针。

重复以上步骤，直到返回空指针或搜索完前缀的最后一个字符。
若搜索到了前缀的末尾，就说明字典树中存在该前缀。此外，若前缀末尾对应节点的isEnd为真，则说明树中存在该字符串。

代码实现（Go）

type Trie struct {
    children [26]*Trie
    isEnd    bool
}

func Constructor() Trie {
    return Trie{}
}
//插入word
func (t *Trie) Insert(word string) {
    node := t
    for _, ch := range word {
        ch -= 'a'
        if node.children[ch] == nil {
            node.children[ch] = &Trie{}
        }
        node = node.children[ch]
    }
    node.isEnd = true
}
//搜索前缀
func (t *Trie) SearchPrefix(prefix string) *Trie {
    node := t
    for _, ch := range prefix {
        ch -= 'a'
        if node.children[ch] == nil {
            return nil
        }
        node = node.children[ch]
    }
    return node
}
//搜索word是否存在
func (t *Trie) Search(word string) bool {
    node := t.SearchPrefix(word)
    return node != nil && node.isEnd
}
//判断前缀是否存在
func (t *Trie) StartsWith(prefix string) bool {
    return t.SearchPrefix(prefix) != nil
}

复杂度分析

• 时间复杂度：初始化操作为O(1)，其余操作为O(|S|)，其中|S|是每次插入或查询的字符串的长度。
• 空间复杂度：O(∣T∣⋅Σ)，其中|T|为所有插入字符串的长度之和，∑为字符集的大小